NV Center Diamonds
Quantum properties of NV diamonds
Optical properties of the NV centre
The first observations of NV centres date back some 50 years [1] and its isolation on an individual scale was not achieved until the 90s. It was first used as a source of single photons [3,4], and then it was found that this defect also possessed spin properties, which made it possible to use it as a quantum bit or a magnetic field sensor.
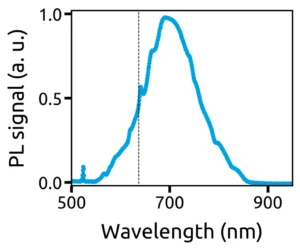
Under optical excitation by a green laser, the NV centre emits stable red photoluminescence at room temperature [2]. In the photoluminescence emission spectrum shown in figure opposite, the zero-phonon line at 637 nm can be observed, which corresponds to the optical transition. The coupling to the phonons of the crystal lattice induces a broad satellite band up to 800 nm.
In the following, we will focus on ensembles of NV centres, with a typical density of a few tens of parts per billion (ppb), hosted in bulk diamonds.
Optical detection of the magnetic resonance
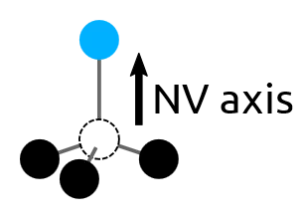
The NV centre has a spin S = 1 in its ground state, so its fine structure is composed of the states |ms = 0> and |ms =± 1> [Fig. 2]. Here, ms is the projection of the spin along the quantization axis of the NV centre, formed by the nitrogen atom and the gap, along one of the [111] crystal orientations of diamond [Fig. 3]. |ms = 0> state is separated from the degenerate |ms =± 1> by D = 2,87 GHz.
The photophysics of the NV centre is governed by spin polarisation and spin state dependent photoluminescence mechanisms [5]. First, under continuous laser excitation, the NV centre will gradually polarise into the |ms = 0>, spin state, thanks to an optical pumping mechanism. Moreover, the |ms = 0>, state emits more photoluminescence than the |ms =± 1>, states, the level of photoluminescence of the NV centre is indicative of its spin state.
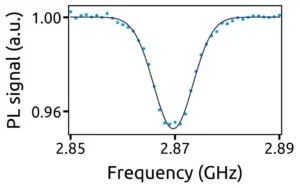
These two properties are at the core of the optical detection of the magnetic resonance of the NV centre. It can be all-optically initialized in its spin state |ms = 0>, and the reading of its spin state is done by measuring the photoluminescence signal. By applying a resonant radio frequency excitation with the |ms = 0> ↔ |ms = ±1> transition, a population transfer between these two spin states will lead to a drop in the photoluminescence signal, as observed in figure 4.
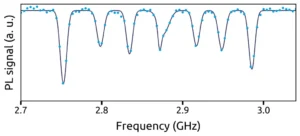
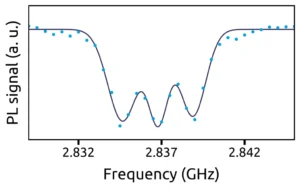
In the presence of a magnetic field with a component that follows the quantization axis of the NV centre, the degeneracy of the |ms = ±1> states is lifted, by the Zeeman effect. The separation between the |ms = +1> and |ms = -1> states is proportional to the field component B//, which makes the NV centre a magnetometer at an atomic scale. In figure 5, 8 lines can be observed in the magnetic resonance spectrum, which correspond to the four |ms = 0> ↔ |ms = ±1> transitions in the four [111] crystal orientations of diamond.
Looking more closely at one of these lines in the magnetic resonance spectrum, the hyperfine structure of the NV centre can be revealed. This structure results from the interaction between the electron spin of the defect and the nuclear spin of the nitrogen atom. Nitrogen 14N has a natural abundance of 99.6% and has a nuclear spin I = 1, which leads to three hyperfine lines [Fig. 6].
Longitudinal relaxation time T1
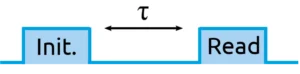
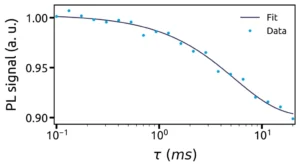
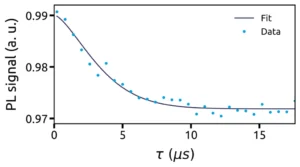
The longitudinal relaxation time, or T1, is the time it takes for the system to return to a thermodynamic balance state once it has been polarised to its spin state |ms = 0>.The standard T1 measurement sequence is shown in Figure 7. It consists of a first initialisation laser pulse, in order to polarise the system into the spin state |ms = 0>, followed by a free evolution time, in the dark, of variable duration τ. The last step is a readout laser pulse, which extracts the spin state of the NV centre via the photoluminescence signal.Figure 8 shows the evolution of the photoluminescence signal as a function of the free evolution time τ in the dark. For short durations τ, the system does not have time to return to its thermodynamic balance state. It remains polarised in its spin state |ms = 0>, which results in a high photoluminescence signal. The gradual relaxation of the system towards its thermodynamic balance state results in the fall in photoluminescence for longer times τ.Fitting the data by an exponential decay allows us to extract the longitudinal relaxation time T1 of 5.4 ± 0.5 ms, which is typical of an NV centre ensemble in a bulk diamond [6]. The T1 time is limited by the interactions between the NV centre and the phonons in the crystal lattice [6].Coherent control of spin state: Rabi oscillations
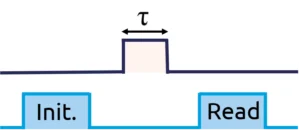
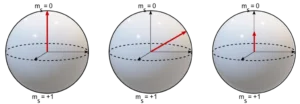
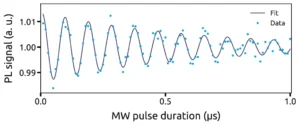
In the following, a bias magnetic field of a few mT will be applied along the quantization axis of the NV centre, in order to lift the degeneracy between the |ms = ±1> states. We will only consider a two-level system, composed of the states |ms = 0> and |ms = +1>.Coherent control of the spin state of an NV centre can be achieved by performing Rabi oscillations between the states |ms = 0> and |ms = +1> [7]. The sequence used is shown in Figure 9.It consists of a first initialization laser pulse, which polarizes the NV centre into its spin state |ms = 0>. This is followed by a radio-frequency pulse of variable duration τ, resonant with the transition |ms = 0> ↔ |ms = +1> : this is the manipulation step. The spin state after this step is a superposition of state α|ms = 0> + β|ms = +1>. The spin state of the system is then extracted by a final readout laser pulse. The Bloch sphere representation of each step is shown in Figure 10.A typical Rabi oscillation signal is shown in Figure 11. For very short microwave pulse durations, the populations do not have time to switch from the |ms = 0> state to the |ms = +1> state, the photoluminescence signal remains maximum. For a radio frequency pulse duration Tπ, a population maximum of the |ms = 0> state has switched to the |ms = +1> state, so the photoluminescence signal is minimum. The coherent oscillations between these two states are represented by the oscillations of the photoluminescence signal. These Rabi oscillations allow us to define the times Tπ and Tπ/2, which are at the heart of the spin dynamics sequences.Transverse coherence time T2*
Decoherence is the loss of quantum information of a system initially placed in a state of quantum superposition,
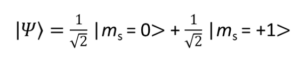
This decoherence is characterised by the transverse coherence time T2*.
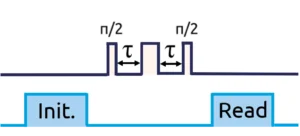
This T2*decoherence time can be measured by the Ramsey fringe method. The sequence is shown in Figure 13. The manipulation step consists of a first radio frequency pulse of duration Tπ/2 to place the system in a superposition state, as described by the equation above.
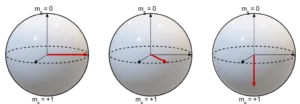
The system then evolves freely for a time τ and will perform a free precession. The coherences will accumulate a phase, which depends on the environment of the NV centre and in particular on the magnetic fluctuations of the spin bath. Finally, a second radio-frequency pulse of duration Tπ/2, followed by the readout laser pulse allows the spin state of the system to be read out. This spin state manipulation step is shown on the Bloch sphere in Figure 14.
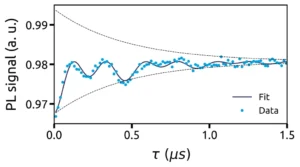
A typical Ramsey fringe measurement is plotted in Figure 15. The decay of the oscillations corresponds to the transverse coherence time T2*, which can be extracted by fitting these data [8, 9], to give a T2* time of 456 ± 45 ns. The decoherence of the NV centre is governed by the interactions with the spin bath, composed of :
- Nuclear spins, such as 13C atoms [8], with a natural abundance of 1.1% and a nuclear spin
I = 1. - Electronic spins, such as nitrogen impurities [9].
- Electron spins on the surface of diamond [10].
This coherence time can be extended by so-called dynamic decoupling sequences, which isolate the system from the magnetic noise generated by the surrounding spin bath.
Dynamic decoupling: coherence time T2echo
The simplest dynamic decoupling sequence to implement is the Hahn echo sequence [11]. As schematised in Figure 16, the handling phase is similar to that presented above for the T2* time measurement, except that a radio frequency pulse of duration Tπ is applied in the middle of the free precession time. The phase shift accumulated during the time τ/2 is thus compensated by the phase accumulated during the second free precession time τ/2, as shown on the Bloch sphere in Figure 17. This method avoids the slow fluctuations of the spin bath, thus extending the coherence time.A typical T2echo time measurement is plotted in Figure 18. Fitting the data with an exponential decay to the power n [10] allows a T2echo lifetime of 3.8 ± 0.2 µs to be extracted.References
[1] Davies, Proceedings, 1976
[2] Gruber et al., Science, 1997
[3] kurtsiefer, PRL, 2000
[4] Brouri, Optics Letters, 2000
[5] Tetienne, New journal of Physics, 2012
[6] Jarmola, PRL 108, 2012
[7] Jelezko, PRL 92, 2004
[8] Maze, New Journal of Physics, 2012
[9] Bauch, Physical Review B, 2020
[10] Rondin, Physical Review B, 2010
[11] Hahn, Physical Review, 1950
NV center diamonds and their production
A diamond is an organised assembly of carbon atoms, transparent to visible light.
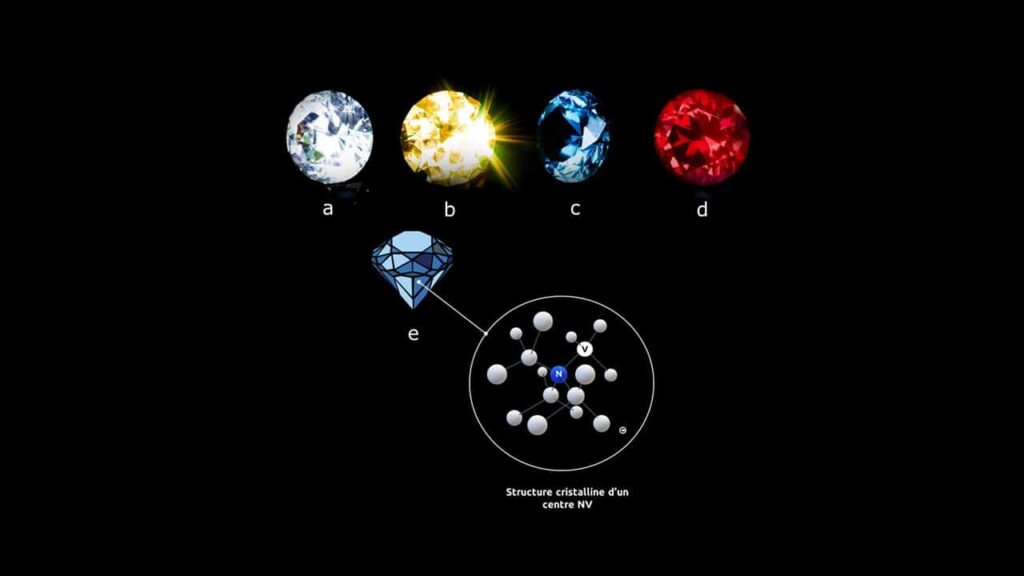
There are many natural diamond hues, often sought after in jewellery (Figure 1a-d), which are due to impurities and defects in the carbon structure that absorb light.
The nitrogen-vacancy center
Amongst these numerous coloured defects (more than 500 are listed [1]), the Nitrogen-Vacancy center or NV has unique properties.
An NV center (see Figure 1d) consists of a nitrogen atom (N) that has been substituted for a carbon atom, and a neighbouring atom site that is left vacant (V).
The NV center can be thought of as an artificial molecule trapped in a solid diamond. It is therefore easy to manipulate, and extremely small (a few Angstroms).
The propertries of a NV center
The NV center is a perfectly stable single photon source.
When illuminated by green light, the NV center re-emits red photoluminescent light.
Unlike many pigments or molecules, the NV center never disappears. This makes it the luminescent marker of choice for biology [2].
Furthermore, a single NV center emits single photons, one after the other. This property makes the NV center an ideal candidate as a light source for quantum optics, and it has been used in fundamental tests such as the Wheeler delayed choice experiment [3, 4].
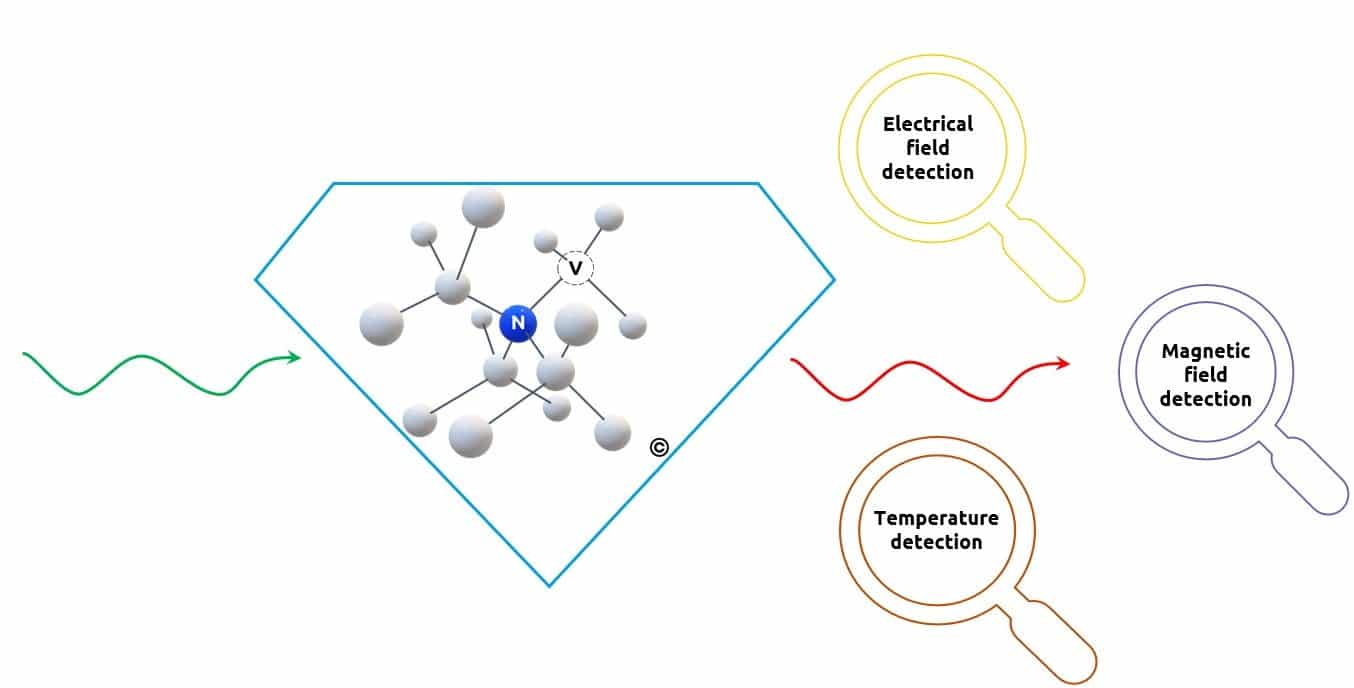
In addition to its optical properties, the NV center has unique spin properties.
A spin is the quantum-scale equivalent of a tiny magnet, like the needle of a compass. When illuminated with green light, the spin of the NV center can be prepared in a desired state.
On the other hand, one can directly read the spin state of the NV center by looking at the amount of red light it emits.
By preparing the spin of the NV center in a known state, we can study its interaction with the environment. This is done by optically measuring the evolution of its state under different conditions of temperature, magnetic field or electric field.
In this way, the NV center is used as a quantum sensor, which can measure various quantities very precisely and with atomic resolution.
The production of NV center diamonds
In order to use the NV center, it is important to be able to control its production.
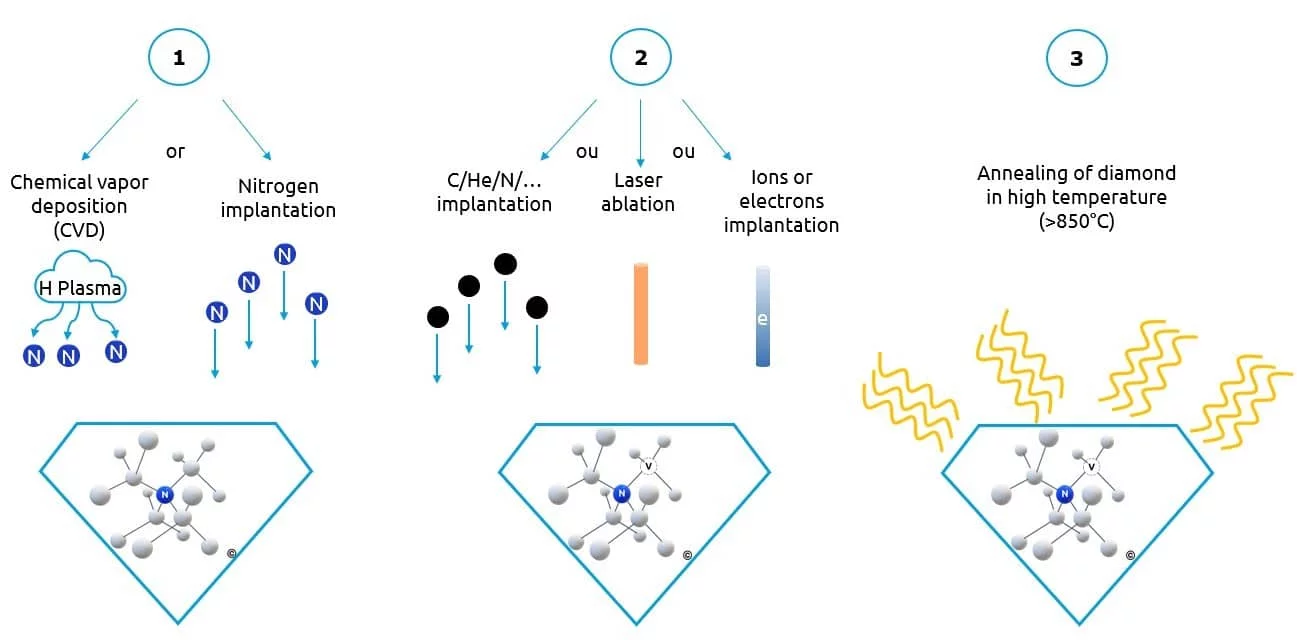
The NV center occurs naturally in most diamonds due to the abundance of nitrogen in the air.
However, in order to have sufficient densities of these centers, or to control their position, the diamond must be doped with nitrogen.
This can be done either by adding nitrogen during the creation of a diamond by chemical vapour deposition (CVD) or by implanting a diamond with nitrogen to modify it.
In both cases, it is then necessary to create gaps in the diamond, i.e., remove some carbon atoms. This can be done by laser ablation, or by implanting the diamond with ion or electron beams.
The final step is annealing the diamond, at high temperature (> 850°C), to rearrange the diamond matrix and promote the migration of vacancies to the nitrogen atoms and obtain NV centers.
In this way, it is possible to have diamonds that are highly doped with NV centers, and to control their position in the diamond [5], in order to manufacture them according to the targeted applications.
References
[1] Zaitsev A. M., Optical Properties of Diamond (2001)
[2] Yuen Yung Hui et al 2010 J. Phys. D: Appl. Phys. 43 374021
[2] Jacques, Vincent; Wu, E; Grosshans, Frédéric; Treussart, François; Grangier, Philippe; Aspect, Alain; Roch, Jean-François (2007). “Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment”. Science. 315 (5814): 966–8.
[3] Wikipédia
[5] Smith, Jason M., Meynell, Simon A., Bleszynski Jayich, Ania C. and Meijer, Jan. “Colour centre generation in diamond for quantum technologies” Nanophotonics, vol. 8, no. 11, 2019, pp. 1889-1906.
J Achard et al 2020 J. Phys. D: Appl. Phys. 53 313001, https://iopscience.iop.org/article/10.1088/1361-6463/ab81d1